지난 글에서 프랙탈에 대한 간단한 개요를 중심으로 프랙탈아트 작품을 소개했다면 이번 글에는 좀더 프랙탈에 관한 이야기를 중심으로 작품들을 소개하고자 한다. 프랙탈이 수학적인 요소에서 출발하였으나, 최근 화려한 색과 현란한 모양으로 뭇 디지털 아티스트들의 가슴을 설레게 만들고 있는 것은 사실이다. 프랙탈을 이야기 하다 보면 자주 테셀레이션과 비교 질문을 받곤 한다. 테셀레이션(tessellation)이란, 우리가 흔히 볼 수 있는 유리창문의 창살 및 욕실이나 마루 바닥에 깔려 있는 타일과 같이 틈이나 교차점 없이 평면이나 공간을 도형으로 덮는 형태(모양)를 말한다. 대표적인 테셀레이션 작가로는 모리츠 코르넬리스 에셔(Maurits Cornelis Escher) 이다. 에셔는 수학적 소재라 할 수 있는 테셀레이션을 예술적 경지로 발전시켰다. 아래의 테셀레이션 그림이나(좌) 혹은 에셔의 작품을 무한대로 확대(Zoom In) 하다 보면 원래의 이미지나 도형은 사라지게 된다. 이것은 자기 유사성을 가진 프랙탈(아래 작품 오른쪽)과는 다른 것이다. 프랙탈은 아래 프랙탈작품(우)에서 보듯이 무한히 확대해도 작은 소용돌이가 지속적으로 나타나게 되므로 이미지 형태가 변하지 않는다.

우리는 생활 속에서 많은 현상들을 보곤 한다.
주위에서 느끼는 이런 현상들 중에서 불규칙 적이고 무질서한 것들을 발견하게 된다.
나무, 해안선, 구름, 산, 태풍, 돌개바람, 담배연기 등등 이런 것들은 자연현상 속에서 무질서한 현상 및 상태를 나타낸다. 이런 혼돈과 무질서는 인간의 지식으로 정의를 내리기 힘든 것이 사실이다. 70년대부터 활발해진 이런 혼돈에 관한 연구가 Chaos 및 Fractal등으로 발전해 가고 있다. 영국의 해안선 길이는 얼마일까? IBM의 토머스 왓슨(Thomas J. Watson)연구센터의 만델브로트(BenoitMandelbrot)는 프랙탈 이론의 창시자라고 할 수 있으며, Fractal(프랙탈)이라는 말을 만들어 낸 장본인이다.
처음 그의 논문이 네이쳐지에 실렸을 때는 그리 주목을 받지 못하다 한다. 그러던 것이 70년대 후반에 이르러서 프랙탈이 뜨거운 감자가 되자 그때서야 과학자들이 부랴부랴 만델브로트의 논문을 뒤지는 해프닝이 있기도 했다고 한다. 그는 그의 논문(The Fractal Geometry of Nature)에서 심오한 의문을 제기한다. "영국의 해안선 길이는 얼마나 될까?" 라는 것인데 이 넌센스 같은 질문은 그 후 많은 논문의 지침이 되기도 했다.
반지름 1인 원의 원주의 길이를 구하는 방법을 생각해보면 고등학교 수학시간에 배운 원주 공식(2Πr)을 적용하면 된다.
Π(파이) = 3.14159.... 이므로 2Πr는 대략 6.28이 된다.
영국의 해안선을 알기 위해서 같은 방법으로 아래의 그림과 같이 적용 할 수 있다.

즉, 곡선의 길이를 잘게 쪼갠 직선의 길이의 합으로 가정하여 계산하는 방법은 측량기사가 지형도를 만들 때 사용하는 절대적으로 확실한 절차다. 아래의 표를 자세히 보면 그 이유를 알 것이다.
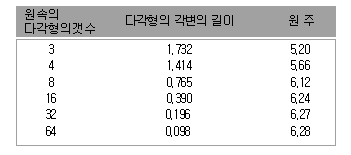
선을 많이 쪼갤수록 2Πr(6.28)에 가까워 짐을 알 수 있을 것이다. 따라서 만델브로트가 제시안 영국의 해안선이 얼마나 되는지 살펴보자.
프랙탈의 창시자는 IBM의 토머스 왓슨(Thomas J. Watson)연구센터의 만델브로트(Benoit Mandelbrot)이다. 그는 Fractal(프랙탈)이라는 말을 만들어 낸 장본인이다. 그는 논문 “The Fractal Geometry of Nature”에서 프랙탈 인식에 관한 간단한 질문을 내놓았다. "영국의 해안선 길이는 얼마나 될까?" 이 질문은 언뜻 보기에는 넌센스 같지만, 이 단순한 질문은 실로 심오한 의문을 제기한 것이다. 그러면 만델브로트가 제시한 영국의 해안선은 얼마나 될까? 아래의 그림은 영국의 해안선을 200마일 단위와 25마일 단위로 잰 것이다. 25마일 단위로 재면 200마일로 단위로 잰 것에 비해서 측정된 해안선의 길이가 길어진다. 그 이유는 해안선은 자세히 보면 볼수록 복잡하기 때문이다. 만일 더 작은 단위로 해안선을 재면 어떻게 될까? 예컨대, 1cm단위로 잰다면 어떨까? 아니, 원자 한 개 길이만한 자로 잰다면 어떨까? 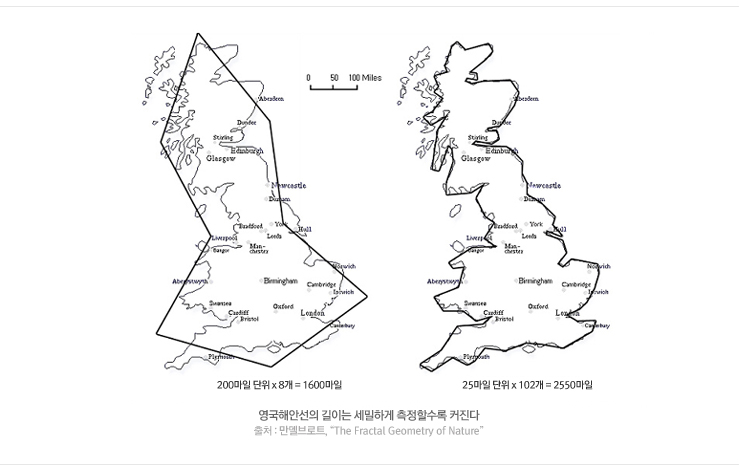
만일 1cm 길이의 측정단위를 사용하여 전 해안선을 기다시피 하며 세밀하게 측정 할 경우, 모든 해안가의 짧은 곡선, 해안 바위들의 굴곡 하나하나가 합산 되어 해안선 측정 값은 엄청나게 증가되어 천문학적인 수치가 나올 것이다.

측정단위에 의해 합산된 곡선의 길이가 단위를 작게 할수록 무작위로 커진다면 그 곡선은 프랙탈 곡선이라고 한다. 따라서 영국의 해안선은 프랙탈이다. 이유는 영국의 해안선은 크고 작은 수많은 만, 내해, 작은 강, 복잡한 바위투성이들로 구성되어 매우 불규칙하기 때문이다. 더욱 짧은 측정단위를 사용하면 구부러진 지형들에 깔끔하게 맞출 수 있으며 이로 인해 전체 길이는 증가하게 될 것이다. 원 모양의 곡선과 영국의 해안선과 같은 곡선은 근본적인 차이가 있다. 이 차이점은 곧 고전적인 기하 형태와 프랙탈 기하 형태는 엄연히 다르다는 사실이다. 그래서, 여기에 첫째 명제가 제기된다. 영국의 해안선은 프랙털이다. 그래서 그 길이를 측정하는 데 따르는 어려움은 프랙탈의 정의를 어떻게 내리느냐 하는 것이다.

영국의 해안선이 프랙탈이라면 우리가 생활하고 있는 주위의 다른 곳에서도 프랙탈을 쉽게 찾을 수 있다. 구름, 산, 나무, 심지어 사람의 뇌의 주름 등에도 프랙탈을 발견할 수 있다.
-계속-

 프랙탈 이야기 3
프랙탈 이야기 3
 프랙탈 이야기 1
프랙탈 이야기 1












Facebook 댓글